Graph Embedding 101: Unraveling the Magic of Relational Data

Graphs are everywhere, from the intricate web of neurons in our brains to the sprawling networks of social media platforms. But how do we translate these complex structures into a language that AI models can understand?

In this post, we'll delve deep into the world of graph embeddings, drawing parallels with familiar concepts, and exploring the challenges and potential of this transformative technique.

What is Graph Embedding?

In short, graph embedding vectorizes nodes.

Imagine a vast, sprawling city - a tangled web of streets and junctions. Each intersection is a point of interest, and each road between them is a connection. Now picture looking down on this city from above - you see a complex mess of intersections and streets spreading out in all directions.

This city is like a graph - a set of nodes (the junctions) and edges between them (the streets). Handling very large, complex graphs tends to be computationally demanding, just as navigating a vast city can be overwhelming.

This is where graph embedding comes in - it takes this vast graph and simplifies it down into a simpler space as if we squeeze all the myriad streets and intersections down into basic proximity on a 2D map. Nodes highly interconnected end up clustered together, just as related city sights group together on a tourist map. Each node gets converted into a single point on a map, represented by coordinates in a lower-dimensional space. Nearby nodes in the original graph end up close together on the map. Far away nodes end up far apart.

So in summary, graph embedding takes a hairball graph and simplifies it down into a tidy map - a vector space that preserves the structure and relationships from the original graph. This is mathematically equivalent to sentence embeddings applied to graphs instead of sentences. In essence, graph embedding vectorizes nodes like sentence embeddings vectorize sentences. It massages graphs into a format friendly for machine learning models.

Formal Definition of Graph Embeddings

Formally, a graph $G = (V, E)$ is a representation of relationships using nodes $V$ and edges $E$. Now, navigating a city can be overwhelming due to its vastness. Similarly, handling large graphs can be computationally challenging. Enter graph embedding.

Graph embedding is the art of translating this city (or graph) into a simplified map, where each point of interest (or node) is represented by a coordinate in a lower-dimensional space. Mathematically, it's about learning a function $f: v_i → y_i ∈ R^d$ that maps each node $v_i$ to a vector $y_i$ in a space $R^d$ where $d$ is much smaller than $|V|$.

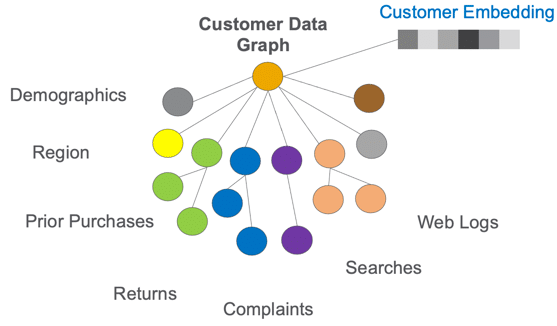
Why is Graph Embedding a Game-Changer?

From predicting potential friendships on social media to visualizing intricate datasets, graph embeddings are proving invaluable. They're pivotal in node classification tasks, link predictions, and even in clustering nodes with similar properties. Moreover, as we venture into the realm of multimodal AI, where different types of data converge, graph embeddings can serve as a bridge, connecting structured data with unstructured data.

1. Machine Learning Compatibility: Traditional ML models, from linear regressors to deep neural networks, thrive on numerical data. Graph embeddings translate the intricate relationships of a graph into a numerical format, making them digestible for these models.
2. Preserving Topology and Features: A well-crafted graph embedding retains the original graph's structure and node features. This dual preservation is a challenge that many earlier methods struggled with.
3. Dimensionality Reduction: Instead of grappling with a dimension for every node, we can now work in a much-reduced space, often just 50-1000 dimensions. This simplification is a boon for computational efficiency.
4. Unearthing Latent Patterns: Beyond the explicit, graph embeddings can tease out hidden relationships, offering insights that might not be immediately apparent in the original graph.

How to Compute Graph Embeddings?

Graph embedding techniques are as diverse as the graphs they seek to represent. However, most can be bucketed into a few broad categories:

• Matrix Factorization: Techniques like HOPE and Laplacian Eigenmaps revolve around factorizing the graph's adjacency matrix A. For instance, HOPE employs a generalized SVD to approximate A as Y_s Y_t^T, extracting the embedding Y in the process.

Asymmetric Transitivity Preserving Graph Embedding

Key words: graph embedding, asymmetric transitivity, Generalized SVD (GSVD)

Ziwei ZhangEmail

Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering

NeurIPS Proceedings

• Random Walks: Picture a drunken walk through our earlier city analogy, meandering through landmarks. Methods like DeepWalk and node2vec use such random walks to capture the essence of a graph. These walks are then fed to models akin to Word2Vec to derive the embeddings.

DeepWalk: Online Learning of Social Representations

We present DeepWalk, a novel approach for learning latent representations of vertices in a network. These latent representations encode social relations in a continuous vector space, which is easily exploited by statistical models. DeepWalk generalizes recent advancements in language modeling and un…

arXiv.orgBryan Perozzi

node2vec: Scalable Feature Learning for Networks

Prediction tasks over nodes and edges in networks require careful effort in engineering features used by learning algorithms. Recent research in the broader field of representation learning has led to significant progress in automating prediction by learning the features themselves. However, present…

arXiv.orgAditya Grover

• Neural Networks: The neural revolution hasn't spared graph embeddings. Approaches like GraphSAGE and GCNs employ neural encoders, which, when applied to a node's local neighborhood, distill both the graph's topology and node features into the embeddings.

Inductive Representation Learning on Large Graphs

Low-dimensional embeddings of nodes in large graphs have proved extremely useful in a variety of prediction tasks, from content recommendation to identifying protein functions. However, most existing approaches require that all nodes in the graph are present during training of the embeddings; these…

arXiv.orgWilliam L. Hamilton

Semi-Supervised Classification with Graph Convolutional Networks

We present a scalable approach for semi-supervised learning on graph-structured data that is based on an efficient variant of convolutional neural networks which operate directly on graphs. We motivate the choice of our convolutional architecture via a localized first-order approximation of spectral…

arXiv.orgThomas N. Kipf

A Toy Implementation of Graph Embeddings

Implementing graph embedding techniques from scratch can be challenging. The algorithm below shows a simple way to generate graph embeddings. It takes an adjacency matrix as input, which represents the connections in a graph. Each row and column corresponds to a node, and a 1 indicates an edge between those nodes.

from typing import List 
import numpy as np

def graph_embedding(adj_matrix: List[List[int]], emb_size: int = 16) -> List[np.ndarray]:
    """Generate graph embedding
    
    Args:
        adj_matrix: Adjacency matrix as nested list
        emb_size: Size of embedding vectors
        
    Returns:
        List of numpy arrays as node embeddings
    """
        
    # Initialize empty embeddings
    embeddings = [np.random.rand(emb_size) for _ in adj_matrix]
    
    # Train embedding -visualize nodes moving closer if connected
    for _ in range(100): 
        for v1, row in enumerate(adj_matrix):
            for v2, is_connected in enumerate(row):
                if is_connected:
                    # Move embeddings closer if nodes connected
                    embeddings[v1] -= 0.1 * (embeddings[v1] - embeddings[v2])  

    return embeddings

• It initializes an embedding vector of random values for each node. Then it trains these embeddings by iterating through the adjacency matrix to identify connected nodes.
• For any pair of nodes that are connected, it moves their embedding vectors slightly closer together. This is done by subtracting a fraction of their vector difference from the first node's embedding.
• Over multiple iterations, nodes that are tightly interconnected will have very similar embedding vectors, while disconnected nodes will remain far apart in the embedding space.
• The for _ in range(100) loop controls the number of training iterations. More iterations allow the embeddings to converge closer to their optimal values for representing the graph structure.

Finally, the embeddings are returned as a list of numpy arrays. Each array is the vector representation for a node.

Top 3 Open Source Packages for Graph Embeddings

This algorithm above gives a simple illustrative example of how graph embeddings can capture topology, which is not recommended to use in production of course. Instead, there are several excellent open source packages available to make working with graph embeddings much easier. Here are 3 popular options:

PyTorch Geometric

PyTorch Geometric is a geometric deep learning extension library for PyTorch. It includes a wide range of graph embedding techniques including GCN, GAT, GraphSAGE, and more. The mini-batches and autograd support make PyTorch Geometric great for developing and training new graph embedding models.

PyG Documentation — pytorch_geometric documentation

Deep Graph Library (DGL)

DGL is a Python package from AWS that provides building blocks optimized for deep learning on graphs. DGL supports inductive graph representation learning techniques like GraphSAGE and GAT out of the box. The flexible frameworks allow you to implement custom graph neural network architectures.

Deep Graph Library

Library for deep learning on graphs

logoThemeix

StellarGraph

StellarGraph is a Python library for machine learning on network data. It has implementations of graph embedding algorithms including node2vec, DeepWalk, and GraphSAGE. StellarGraph integrates seamlessly with common ML frameworks like TensorFlow and Scikit-Learn.

StellarGraph - Machine Learning on Graphs

StellarGraph provides graph analytics software for machine learning on networks. Uncover insights with the next generation of data science tools.

Stellar2

These libraries make it easy to leverage graph embeddings in your own projects. They handle low-level optimizations and provide pre-built models so you can focus on your application. Graph embeddings are now more accessible than ever for researchers and developers.

Graph Embeddings vs. Sentence Embeddings

Graph embeddings and sentence embeddings, both aim to distill intricate structures into compact vector forms, yet they cater to distinct data types and possess their own set of challenges and strengths. Let's embark on an expedition to discern their similarities, differences, and unique attributes.

The Common Ground

• Dimensionality Reduction: Both graph and sentence embeddings endeavor to encapsulate high-dimensional data within a more compact, lower-dimensional space. This transformation not only makes the data more tractable but also primes it for machine learning models.
• Preservation of Relationships: Be it the intricate ties between nodes in a graph or the semantic dance of words in a sentence, both embeddings are committed to ensuring that the spatial relationships in the original structure find their echo in the embedding space.
• Facilitating Machine Learning: By transmuting graphs and sentences into fixed-length vectors, both embeddings pave the way for the application of a plethora of machine learning algorithms, spanning from clustering to classification.

Diving into the Differences

Challenges and the Road Ahead

Graph embeddings, while transformative, are not without their challenges. Striking the right balance between preserving topology and node features is a tightrope walk. As graphs burgeon in size and intricacy, the specter of computational inefficiency looms large. However, as evidenced by initiatives like the RESTORE framework, the community is rallying together, pooling resources and expertise to surmount these challenges.

RESTORE: Graph Embedding Assessment Through Reconstruction

Following the success of Word2Vec embeddings, graph embeddings (GEs) have gained substantial traction. GEs are commonly generated and evaluated extrinsically on downstream applications, but intrinsic evaluations of the original graph properties in terms of topological structure and semantic informat…

arXiv.orgHong Yung Yip

In conclusion, graph embeddings are not just reshaping our understanding of relational data; they are laying the foundation for a future where data, irrespective of its form or source, can be seamlessly integrated and processed. As we continue our foray into the uncharted territories of machine learning, tools and techniques like graph embeddings will be the compass guiding our way. Stay tuned as we journey deeper into the mesmerizing realm of machine learning, uncovering treasures and charting new courses!